应用经验模式分解和互信息来分离信号中嵌入的随机和确定性分量

2023.02.06

如果正在处理的时序数据不完全确定性，我们可以做什么呢

最近看到了一篇论文：

该论文提出了一个框架，在给定时间序列的情况下，将其分解为随机影响和确定性成分。能够生成该分解将允许我们单独对随机分量进行建模。
这里的主要思想是分析应用于时间序列的经验模态分解方法生成的 IMF 的相位谱。

经验模态分解

第一步是将时间序列划分为所谓的本征模态函数（IMF）。为此，需要使用一种称为经验模态分解 (EMD) 的方法，该方法将接收时间序列作为输入，并从中生成 IMF。
IMF 本身就是一个时间序列，满足两个条件：

系列的最大值和最小值的绝对值之差不得大于 1
IMF 的平均值必须为零

EMD 将通过应用以下算法生成这些 IMF：

找到该系列的所有最大值和最小值
使用三次样条对它们进行插值以生成我们所说的包络。对于计算机科学专业的人来说，您可以将其视为 Big O 和 Big Omega 函数
计算该包络的平均值并从中减去原始信号

一旦找到 IMF，就从该 IMF 中减去原始时间序列，生成一个新信号，我们将其称为 h。然后对 h 重复整个过程，直到找到下一个 IMF，然后从 h 中减去，依此类推。

只有找到一个单调的序列（即它只增长或减少），或者换句话说，一个只有一个极值点（最大值或最小值）的序列时，这个过程才会停止。这个系列将被称为residue。

解释 IMF 并对其进行编码

pip install EMD-signal

import numpy as np
from scipy.fft import fft
import matplotlib.pyplot as plt
from PyEMD import EMD
from sktime.datasets import load_airline, load_shampoo_sales
from sklearn.feature_selection import mutual_info_regression
def emd(signal):
    emd = EMD(DTYPE=np.float16, spline_kind='akima')
    imfs = emd(signal.values)
    
    t = [i for i in range(len(signal))]
    N = imfs.shape[0]
    fig, axs = plt.subplots(N + 1, 1, figsize=(15,9))
    axs[0].plot(t, signal)
    axs[0].set_title('Original Signal')
    for n, imf in enumerate(imfs):
        axs[n+1].plot(t, imf)
        axs[n+1].set_title(f'IMF {n}')
    
    return imfs

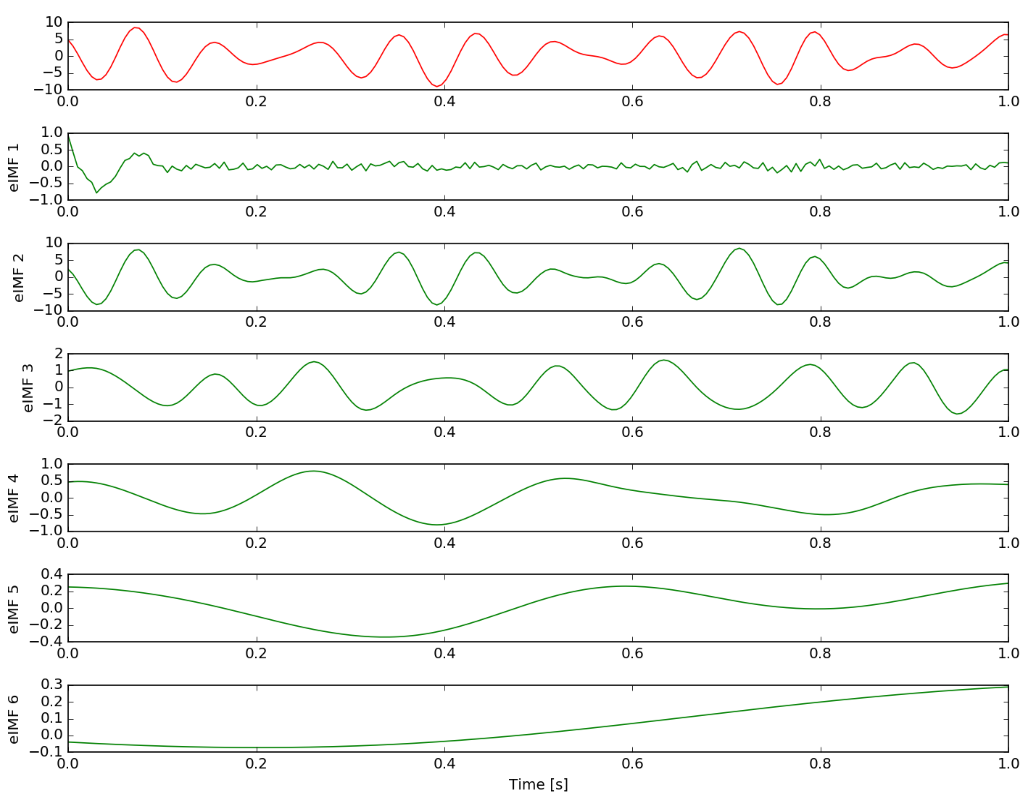
可以看到 IMF6 实际上表现得像残差。

相位谱

生成 IMF 后可以分析每个分量在频谱上的表现。随机信号的频谱遍布各处，没有明确的频率。另一方面，确定性信号的表现会更好。

可视化这一点的一种方法是查看频率空间上这些分量的相位谱，必须首先通过快速傅立叶变换 (FFT) 获得 IMF 的频率表示，然后将虚部除以实部。

def phase_spectrum(imfs):
    imfs_p = []
    fig, axs = plt.subplots(len(imfs), 1, figsize=(15,9))
    for i, imf in enumerate(imfs):
        trans = fft(imf)
        imf_p = np.arctan(trans.imag / trans.real)
        
        imfs_p.append(imf_p)
        
        axs[i].plot(imf_p, 'o')
        axs[i].set_title(f'IMF {i}')
        
    return imfs_p

从图中来看，最后两个组成部分比前两个组成部分更具确定性。

选择具有互信息的 IMF

评估两个分布之间关系的一种方法是互信息。该指标的逻辑是测量一个人可以通过观察另一个变量从一个变量中获得多少信息。

可以应用 IMF 上的互信息并查看它何时出现峰值。从这里应该开始将 IMF 视为确定性成分。

def phase_mi(phases):
    mis = []
    for i in range(len(phases)-1):
        mis.append(mutual_info_regression(phases[i].reshape(-1, 1), phases[i+1])[0])
        
    return np.array(mis)

划分信号

现在就有了将时间序列分成两个部分所需的代码：

def divide_signal(signal, imfs, mis, cutoff=0.05):
    cut_point = np.where(mis > cutoff)[0][0]
    stochastic_component = np.sum(imfs[:cut_point], axis=0)
    deterministic_component = np.sum(imfs[cut_point:], axis=0)
    
    t = [i for i in range(len(signal))]
    
    fig, axs = plt.subplots(3, 1, figsize=(15,12))
    axs[0].plot(t, signal.values)
    axs[0].set_title('Original Signal')
    
    axs[1].plot(t, stochastic_component)
    axs[1].set_title('Stochastic Component')
    
    axs[2].plot(t, deterministic_component)
    axs[2].set_title('Deterministic Component')
    
    return stochastic_component, deterministic_component

定义了将多少互信息视为确定性分量的开始，然后对 IMF 求和并将分量与原始信号一起绘制：

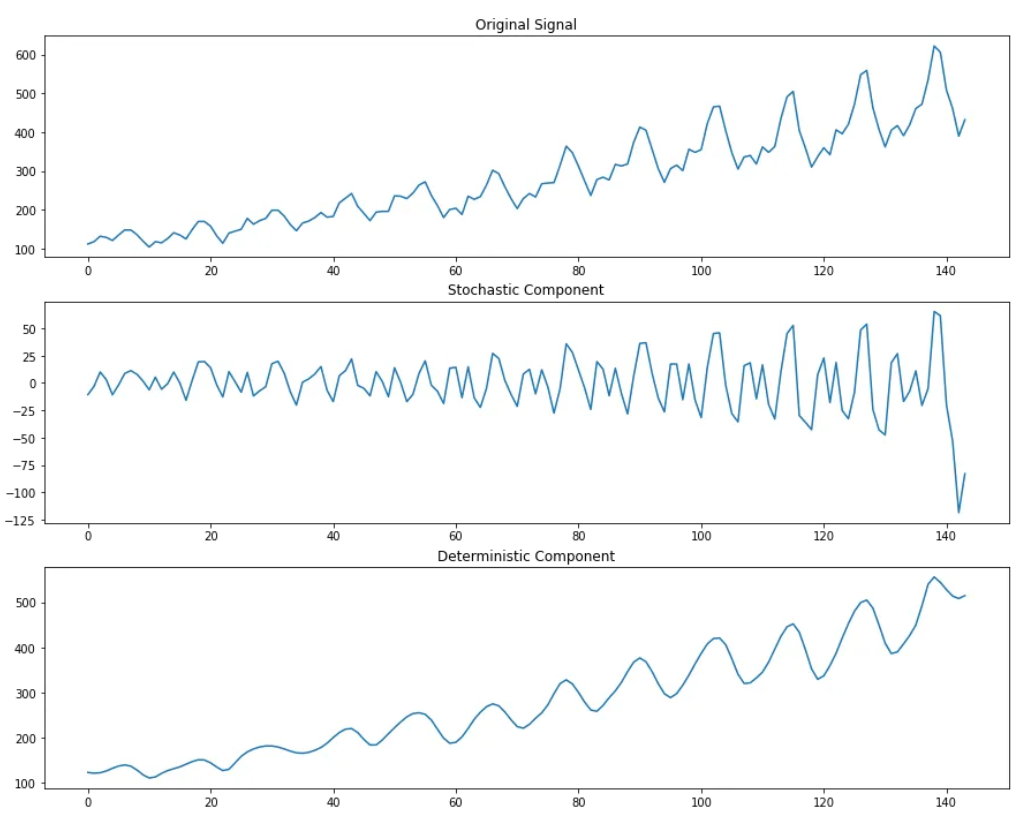
从图上来看，第二行的图表示时序数据的随机分量，第三行数据表示时序数据的确定性分量。

现在，有了这两个分量，我们可以使用 Taken 嵌入定理来预测确定性分量，并使用 ARIMA 等预测器来预测随机分量，以掌握可能仍存在于该组件上的一些确定性残差。

可以用它来改进我们的时间序列分析，将此方法与 Taken 嵌入定理结合使用，就有了一个很好的框架来开始分析和预测时间序列数据。

nlp python 时序数据随机和确定性分量分解

△

Print (Ya Chen); Starry Sky

应用经验模式分解和互信息来分离信号中嵌入的随机和确定性分量

经验模态分解

解释 IMF 并对其进行编码

相位谱

选择具有互信息的 IMF

划分信号