PCA 假设方差是数据集的有趣之处。当数据集中的变量相关时，它们的一些方差是多余的。我们可以用较少数量的新变量（称为主成分）来总结这种协方差。主成分是具有特定属性的原始变量的加权平均值。

将 PCA 应用于2021 年 NFL 球探联合数据集的一个小型双变量子集
NFL 联合赛是一项年度赛事，精英大学运动员会完成一系列测试，为选秀做准备。
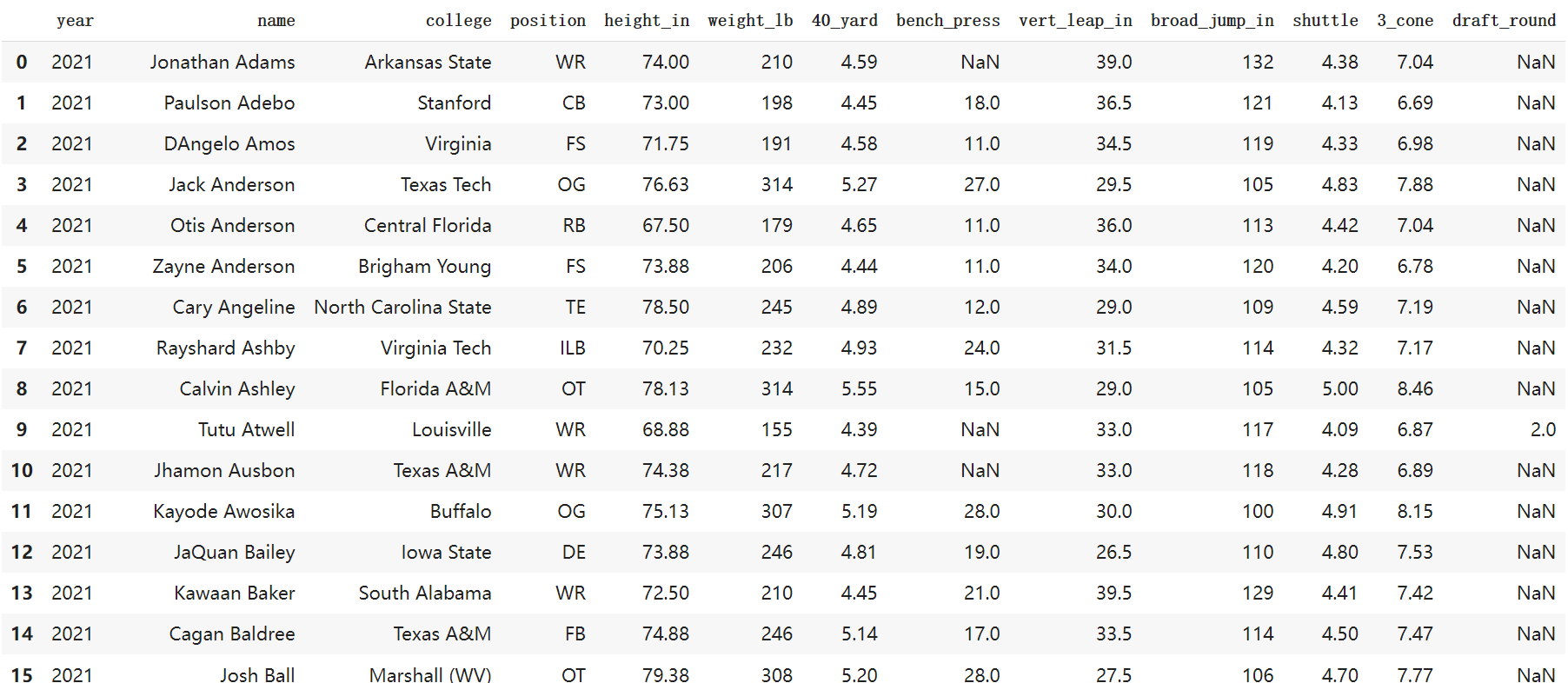
数据大概是下面这样的：

用八维数据集返回到二维 PCA 空间视图

fig, ax = plt.subplots(8, 8, figsize=(15, 15))
for i, feat1 in enumerate(feats):
    for j, feat2 in enumerate(feats):
        # Plot histograms on diagonal
        if feat1 == feat2:
            ax[i][j].hist(df[feat1], color=BLUE, density=True, alpha=0.5)
        # Otherwise plot scatterplots
        else:
            ax[i][j].scatter(df[feat2], df[feat1], color=BLUE, alpha=0.5)
        if i == len(feats) - 1:
            ax[i][j].set_xlabel(name_map[feat2], fontweight='bold', fontsize=FS_FOOTNOTE, color=DARK_GREY, alpha=0.6)
        if j == 0:
            ax[i][j].set_ylabel(name_map[feat1], fontweight='bold', fontsize=FS_FOOTNOTE, color=DARK_GREY, alpha=0.6)
        # Style axes
        ax[i][j].set_xticklabels([])
        ax[i][j].set_yticklabels([])
        ax[i][j].grid(b=True, color=GREY, alpha=0.1, linewidth=3)
        for spine in ['top', 'right', 'left', 'bottom']:
            ax[i][j].spines[spine].set_visible(False)
            ax[i][j].spines[spine].set_visible(False)
            
# Figure level styling
fig.suptitle('Scatterplot scalability', x=0.155, y=1.03, fontweight='bold', fontsize=FS_SUPTITLE)
fig.text(0.012, 0.975, 'The number of pairs scales quadratically with the number of variables', fontweight='bold', color=GREY, fontsize=FS_CAPTION)
fig.tight_layout()
plt.show() 

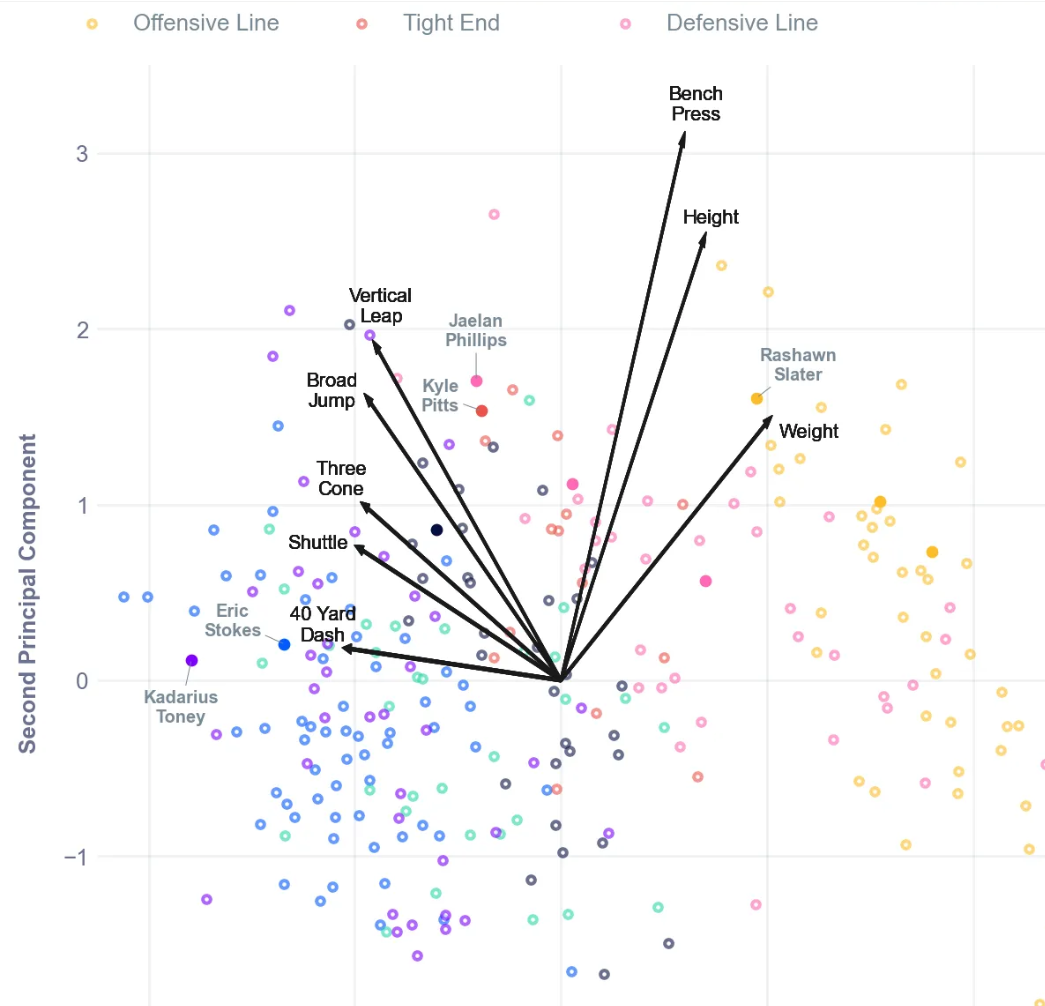
相似方向的向量表示相关变量的簇

还可以查看前两个主成分的载荷，以进一步阐明水平轴和垂直轴的解释。与之前相比，第一个主成分现在主要关注速度和重量之间的权衡，而第二个主成分则关注高度和跳跃能力。

按位置着色，可以看到许多预期的模式，包括接球手和防守后卫的速度和爆发力、进攻前锋的优势体型、进攻后卫的紧凑性以及近端锋的全面性。此外，还重点介绍了一些首轮选秀球员（实心圆圈），他们往往在其位置群体中处于运动极限。

# Filter to feature set
df_temp = df[feats].copy()

# Make larger value "better" for all variables for more intuitive vectors
# This requires negating timed events where larger value is otherwise "worse"
for col in ['40_yard', 'shuttle', '3_cone']:
    df_temp[col] = -1 * df_temp[col]
    
# Standardize features   
ss = StandardScaler()
X = ss.fit_transform(df_temp.values)

# Compute principal components and transform features
pca = PCA()
pca.fit(X)
# Note: we fit on a subset, but need to transform all the data
X = pca.transform(X)

# Add principal components to the dataset for plotting
df['pc1'] = X[:,0]
df['pc2'] = X[:,1]

fig, ax = plt.subplots(figsize=(18, 18))
# Iterate over all positions and plot with distinct colors
for i, pos in enumerate(df['merge_pos'].unique()):
    # Plot athletes who were not drafted in first round
    df_temp1 = df.loc[(df['merge_pos'] == pos) & (~df['draft_round'].isin([1]))].copy()
    ax.scatter(df_temp1['pc1'], df_temp1['pc2'], s=75, label=pos, marker='o', color=COLORS[i], linewidths=4, facecolor=WHITE, alpha=0.6)
    
    # Plot athletes who were drafted in first round
    df_temp2 = df.loc[(df['merge_pos'] == pos) & (df['draft_round'].isin([1]))].copy()
    ax.scatter(df_temp2['pc1'], df_temp2['pc2'], alpha=1.0, s=95, marker='o', color=COLORS[i], linewidths=4)
    
# Plot loadings of the principal components as projected features
comps = pca.components_
comp_weights = list(zip(feats, comps[0,:], comps[1,:]))
scaler = 5 # Basically a shimming factor for how long you want to make the arrows
x_offset, y_offset = 0.4, 0.4 # You can customize these using a map from the features instead
for feat, x, y in comp_weights:
    ax.arrow(0, 0, scaler*x, scaler*y, color='k', width=0.02, alpha=0.6)
    ax.text(scaler*x + x_offset * np.sign(x) * (np.abs(x) / (np.abs(y) + np.abs(x))),
            scaler*y + y_offset * np.sign(y) * np.abs(y) / (np.abs(x) + np.abs(y)),
            name_map[feat],
            ha='center',
            va='center',
            color='k',
            alpha=1.0,
            fontsize=FS_FOOTNOTE)
    
# Style the axes further
for i in range(2):
    for spine in ['top', 'right', 'left', 'bottom']:
        ax.spines[spine].set_visible(False)
ax.grid(b=True, color=GREY, alpha=0.1, linewidth=3)
ax.tick_params(colors=DARK_GREY, labelsize=FS_LABEL, which='both')
plt.setp(ax.get_xticklabels(), alpha=0.6)
plt.setp(ax.get_yticklabels(), alpha=0.6)
ax.set(xlim=(-4.5, 6), ylim=(-2.5, 3.5))
ax.legend(bbox_to_anchor=(0.413, 1.1), ncol=4, loc='upper center', fontsize=FS_LABEL, facecolor='white', frameon=False)

# Style the figure
fig.suptitle('Plotting Eight Dimensions of the 2021 NFL Combine', x=0.061, y=1.02, ha='left', fontweight='bold', fontsize=FS_SUPTITLE, color='k')
fig.text(0.061, 0.97, 'Principal Component Analysis shows 78% of athletic variance across 8 tests using only 2 dimensions', fontsize=FS_CAPTION, color=GREY)
caption = '''
    Notes: Arrows indicate direction and magnitude of variation in superior performance/attribute. Positively
    correlated measurements point in similar directions. Solid circles designate first round draft picks. First-
    round picks are noticeably bigger, faster, and more explosive than most peers in the same positions.
    '''
fig.text(0.061, -0.02, caption, fontsize=FS_CAPTION, color=GREY, linespacing=1.4, fontstyle='italic')
plt.show()