最近在使用GBNC的时序数据，GBNC是什么数据呢，是谷歌将图书数据扫描下来然后经过大数据处理的一个在线词频时序数据搜索框架，还挺有意思的，可以了解一下（https://books.google.com/ngrams/）

但是既然是图书扫描后得到的数据，那很明显在扫描的过程中就可能会出现误差，也就导致了生成时序数据的噪声，所以在做实验前需要消除这些噪声

我找了三个时序数据降噪处理的方法：

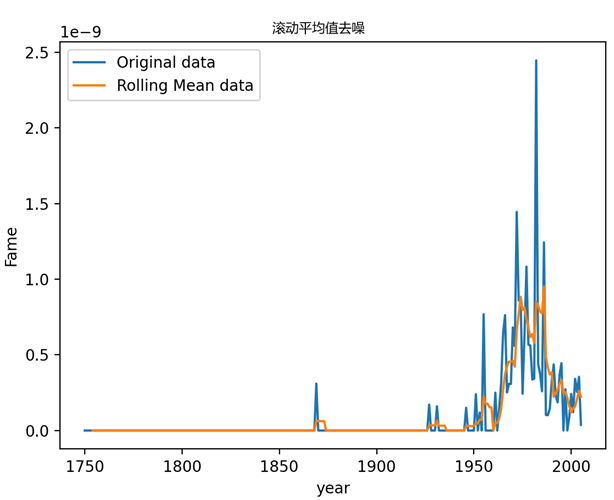
滚动平均值

其中连续m项序列的第一项，是原来n序列的第一项至m项之和除以m；连续m项序列的第二项是原来n序列的第二项至第m+1项之和除以m；滑动平均值为连续m项序列中的第一项至第m项之和除以……连续m项序列的最后一项是原来n序列的第（n-m+1）至第n项之和除以m ；滑动平均值为连续m项序列中的第一项至第m项之和除以……。滑动平均值因项数m的不同而有不同的名称。例如，m为3、5、10，其滑动平均值分别为3年滑动平均值、5年滑动平均值和10年滑动平均值。

df_rollingMean = pd.DataFrame()
for i in range(1,19):
    rolling = data.iloc[:,i].rolling(3).mean()
    # print(rolling)
    df_rollingMean = pd.concat([df_rollingMean,rolling],axis=1)
    # plt.plot(data['year'], data.iloc[:,1])
    # plt.plot(data['year'], rolling)
    # plt.xlabel('year')
    # plt.ylabel('Fame')
    # plt.legend(['Original data','Rolling Mean data'])
    # plt.show()
print(df_rollingMean)
df_rollingMean.to_excel('powerLaw_data.xlsx',sheet_name="rollingMean")

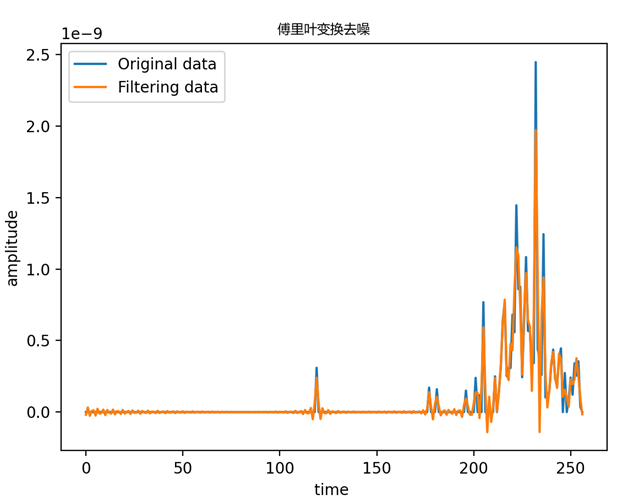
傅里叶变换

傅里叶变换是一种强大的工具,可以用于降噪。通过将信号分解成不同频率的成分,我们可以使用滤波器或频域滤波来去除噪声。

data = data['C. R. Madeley'].tolist()
plt.plot(data,label="Original data")
plt.xlabel('time ')
plt.ylabel('Fame')
y = fft(data)
# threadhold越小，删除的数据就越多
threadhold = 100
y[threadhold:(len(data)-threadhold)] = 0   # 滤波器
data_c = ifft(y)
plt.plot(data_c,label="Filtering data")
plt.legend()
plt.show()

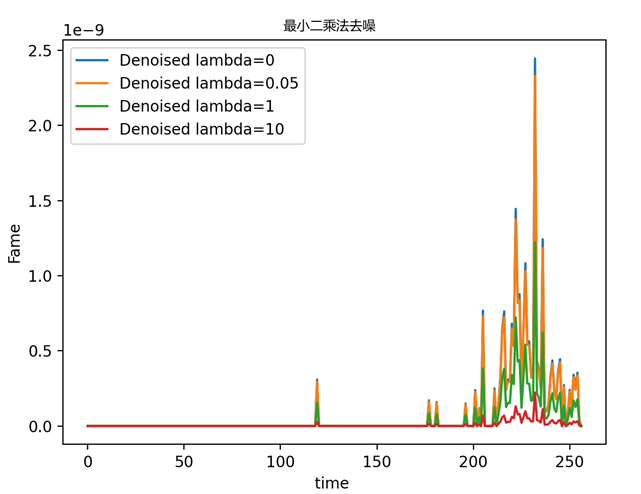
最小二乘法

最小二乘回归算法在降噪中的基本原理:对于一个含有噪声干扰的信号序列,在一定条件下可以通过线性组合的方式来近似表示它。

xlsx_file = "./powerLaw_data.xlsx"
datadf = pd.read_excel(xlsx_file, sheet_name="Original data")
df = pd.DataFrame()
for i in range(1,datadf.shape[1]):
    data = datadf.iloc[:,i].values
    vec = data.reshape(-1,1)
    n = vec.shape[0]
    D = np.zeros((n-1 , n))
    for i in range(n-1):
        D[i,i] = 1
    lambda_list = [0.08] #参数，数值越小对时间序列的影响越小
    x_list = []
    for LAMBDA in lambda_list:
        # Ax = B --> min||Ax-b||^2
        A = np.vstack([np.eye(n), (LAMBDA**0.5)*D])
        b = np.vstack([vec,np.zeros((n-1,1))])
        # Least squares
        # x = INV(X.T* X) * X.T * b
        x = np.matmul(np.linalg.inv(np.matmul(A.T,A)),  np.matmul(A.T,b))
        x_list.append(x)
    # for ind in range(len(lambda_list)):
    #     plt.plot(list(range(len(vec))), data, label="Original data")
    #     plt.plot(list(range(len(vec))),x_list[ind].reshape(-1,) ,label=f'Denoised lambda={lambda_list[ind]}')
    #     plt.xlabel('time ')
    #     plt.ylabel('Fame')
    #     plt.legend()
    #     plt.show()
    # print(x_list[0])
    denoise = pd.DataFrame(x_list[0])
    df = pd.concat([df,denoise],axis=1)
df.to_excel('./powerLaw_denoisedata.xlsx',sheet_name="Denoise data")

总结

总共使用了三种时间序列的降噪方法。滚动平均和GBNC中smoothing的效果一样，所以在这个例子中用来降噪不太合理；傅里叶变换比较多的用在信号降噪上，在处理过程中可能会出现负值，对于这些负值处理不方便；最小二乘法效果比较好，在保留时序数据原有趋势的情况下能够去除一部分的噪声。

通过最小二乘法对时间序列进行拟合，通过拟合曲线去去除时序中的噪声，实现还原时间序列的目的
10个案例，每个案例2个时间序列（coinage/miscrefit），总共20个时间序列


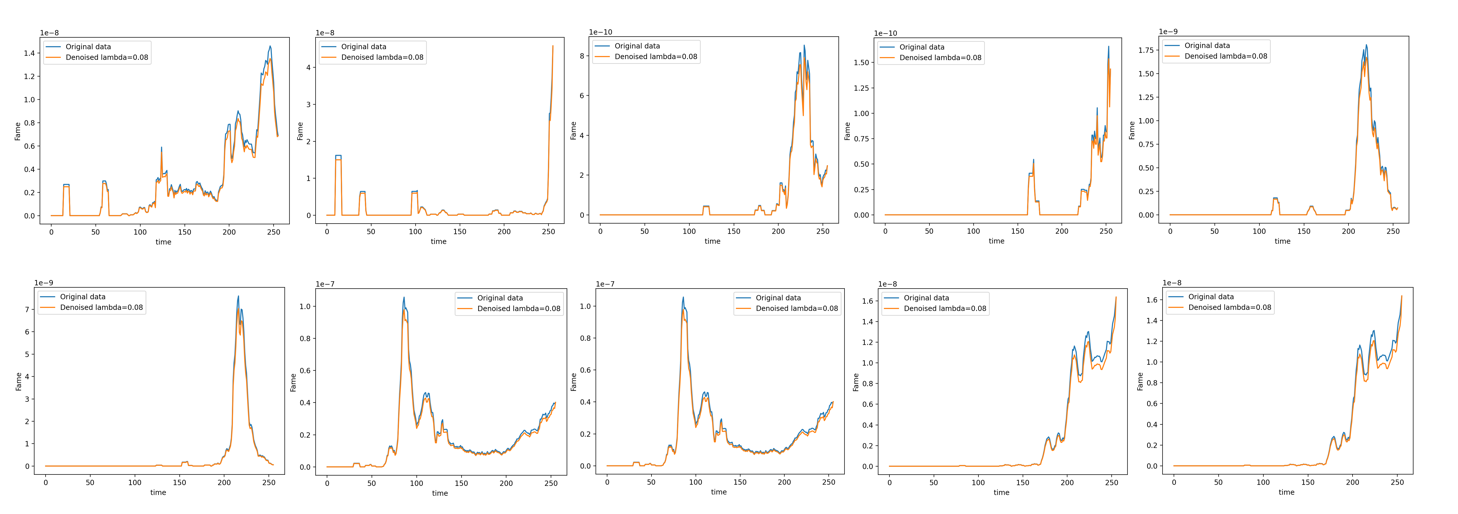
（蓝线表示原始数据，橙色线表示经过降噪后的数据）