一次建模比赛，下面记录一下实验的过程和对实验结果的解读
建模总共分成四个部分，分别对应四个小题：

摘要总结

针对问题1

检测数目为30000人，在最坏情况下从学生群体中确定一个阳性病例。采用多阶段检测方法，各阶段每个试管设置不同的检测人数，依据二分法的思想，通过改进的二分算法设置各阶段每个试管最优的检测人数，以用达到最少检测次数确定一个阳性病例。经过实验测试，不考虑测试阶段次数限制，设置8个阶段，分别为100、50、25、13、7、4、2、1人/管，检测次数最少为314次。

针对问题2

学生在核酸检测后一天感染新冠病毒，计算发现该学生是阳性的平均所需时间。新冠患者经历潜伏期和感染期，假设潜伏期内因为病毒载量不足，无法检测出阳性，当患者进入感染期进行核酸检测，有假阴和阳性确诊两种情况，核酸检测为假阴时需要多轮检测才能最终确定为阳性。考虑学生群体的免疫抵抗力较强，对潜伏期3-7天设置不同的权值，从感染当天开始计算，平均需要9天才能发现学生是阳性。

针对问题3

采用问题二中的平均检测时间作为模型建立前提假设，即在检测到该阳性患者前无法通过核酸检测到该患者的阳性密接患者。建模过程采用仅考虑了易感者和患病者人群的SI模型，同时将密接概率引入传统SI模型作为改进。依据改进的SI模型计算得出当感染概率β分别为90%、30%、5%、1.5%时，感染人数分别为17163人、7194人、1324人、404人。对此根据密接和次密接单独隔离的原则，学校可准备与感染人数相同的隔离房间来进行疫情防控。

针对问题4

基于实际本土疫情数据以及相关文献参考，设置平均接触人数、感染系数、病毒潜伏期等影响因子，使用SEIR传染病模型来拟合分析上海本轮疫情的传播范式。根据封城前后的不同感染系数，借助拟合完成的模型较为准确的模拟出上海不同封城时间结点的奥密克戎病毒传播情况。

具体实验

建模涉及的论文就不在这边流水线的记录了，下面就主要简单记录一下整个建模过程使用到的模型和方法，主要用的都是一些传播学模型，比如SI，SIR等等的，这类模型其实也不算难，就是涉及两个微分方程，对模型进行创新的话也会从两个动力学微分方程上来下手

问题1 最少检测计算

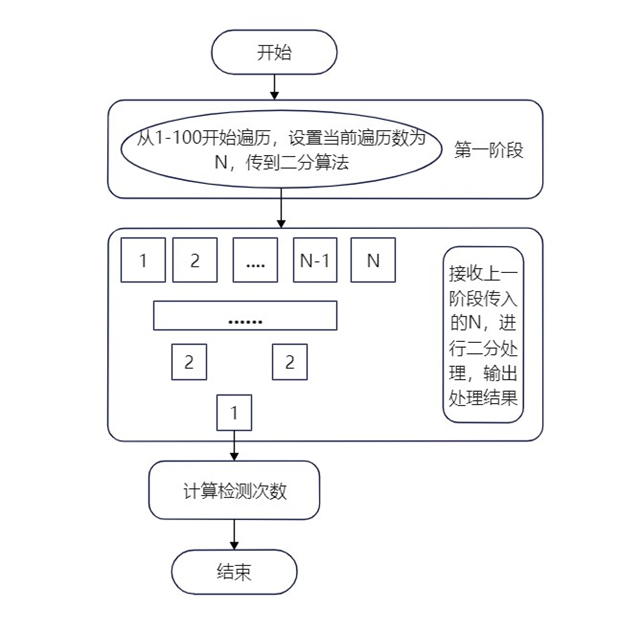
先对问题进行模拟推演，题目要求试管的容量在100以内，第一阶段可选择的试管人数可以是1-100。发现阳性病例的试管后，对该试管的人员进行二次检测，采取二分法的思想，每次平均获取上一级阶段人数的一半，其中N_a表示进行的第a阶段每个试管的检测人数，K_a表示第a阶段需要检测的人数推演过程如下面这个表所示：

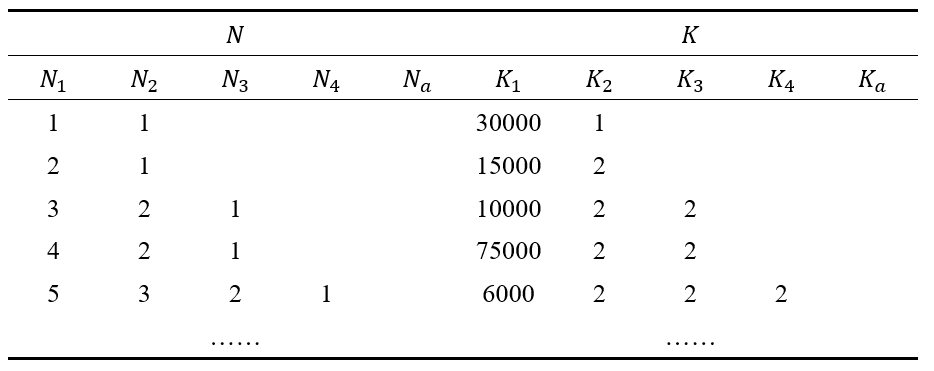
借助Python工具实现代码逻辑，首先遍历从1-100作为第一阶段的数目，再将对应的数进行二分法分解，可以获得最少的检测次数。不考虑检测的阶段次数限制，通过与所有的第一阶段数对比，当设置第一阶段为100时，有最少的检测次数。最终，通过设置8个阶段，能够实现最少的检测次数，只需要检测314次便能够从学校30000人中检测出一例阳性病例

问题2 平均确诊时间

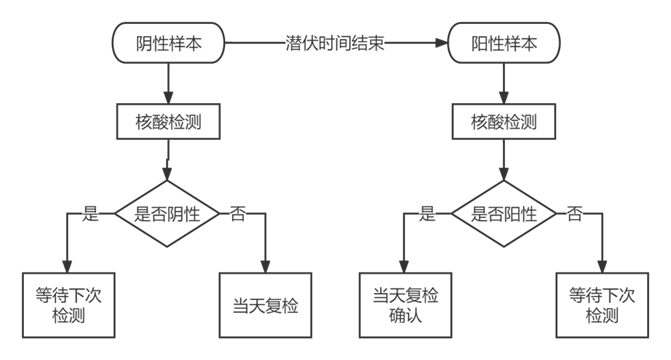
上面这个图是阳性确诊流程图，在实际的应用场景中，感染新冠病毒后检测样本不会立即呈阳性，新冠病毒会有一段潜伏期，并且在潜伏期由于病毒载量不足无法被检测为阳性。我们将潜伏时间设置为计算确诊平均天数的影响因子之一，并根据现实中人群的潜伏期通常为3-7天，可以将其定义为 D_i={3，4，5，6，7} ，依据问题二的分析，假定学生感染新冠病毒当天作为计算平均天数的第1天。

普通人群的潜伏期一般是3-7天，但是身体强壮、健康的群体往往病毒的潜伏时间更长，这也意味着计算发现阳性人群的所需时间也不能将群体都看为是普通群体，需要结合实际情况。依题意计算发现学生是阳性所需花费的平均时间，需要考虑到学生群体主要是处于青壮年时期，群体的免疫抵抗力是远高于儿童和老年群体，基于这种情况，通过参考网络数据和相关文献，将病毒的潜伏期以及相关权值设置如下表

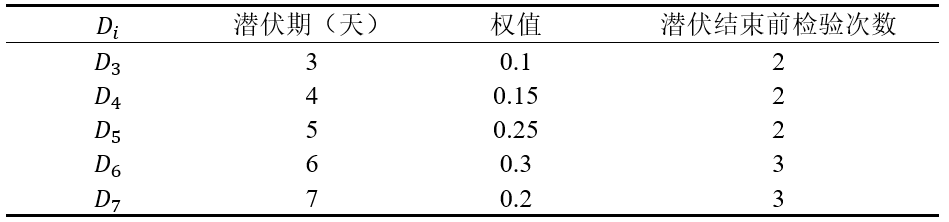
我们需要考虑到当感染新冠病毒之后，由于学生群体的免疫抵抗力较强，病毒的载量不足会导致核酸检测为阴性，潜伏期内学生群体无法检测到新冠病毒。综上所述问题分析和设计测试方案，借助Python工具实现代码逻辑，由题意可知阳性样本中，检测出来是阳性的概率是 p (0.5≤p≤0.7) ，假阴的概率 1-p 。为使计算结果具有较高的准确度，将 p 按照0.01的增幅进行测试，同时每次测试使用10000条数目进行随机检验，得到如下表所示结果。

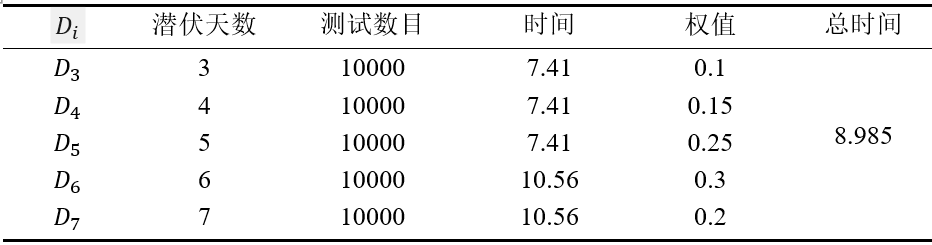
所以如果有一个学生在核酸检测的后一天外出时感染了新冠病毒，且无任何症状，在核酸检测有效期是72小时的情况下，通过学校的核酸检测，发现这个学生是阳性平均需要9天。

问题3 感染人数估计

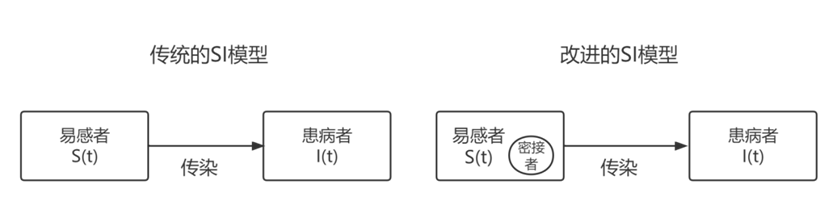
上面是我们设计的改进后的SI模型
在本模型中的假设说明如下所示：
（1）校园总人数为N不变，即不考虑生死或迁移，本模型取30000人作为总人数。
（2）人群分为易感者（S类）和患病者（I类）两类，初始患病者个数为1。
（3）在不同人群的口罩戴取情况下，感染概率β分别为90%，30%，5%，1.5%四种情况。
（4）依据时空伴随思想判断为密接，本模型估算每个人每天密接人数为300人,则密接概率λ为1/1000。
（5）将第t天易感者与患病者两类人群占总人数的比例分别记为s(t)、i(t)，数量记为S(t)、I(t)。

β=90%传染过程图：

β=30%传染过程图：

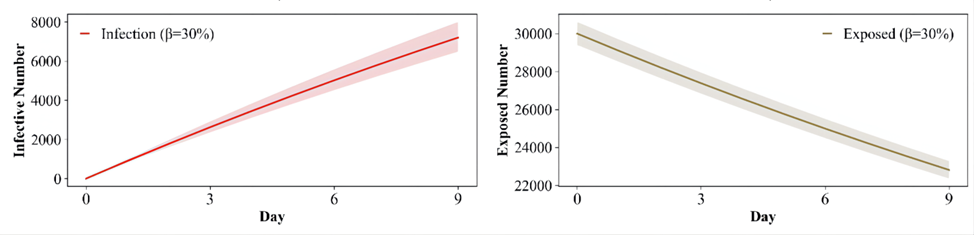
β=5%传染过程图：

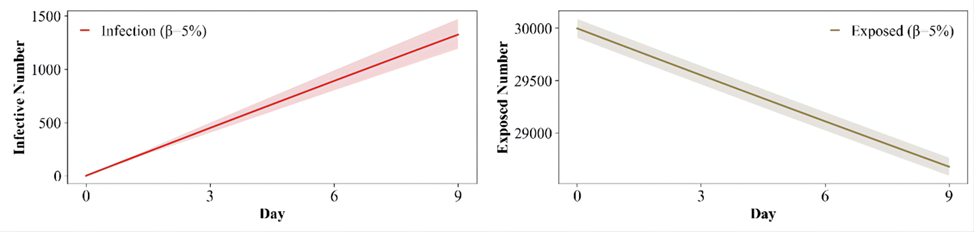
β=1.5%传染过程图：

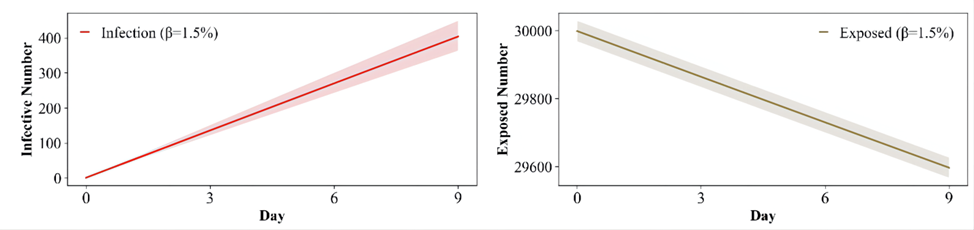
对比建模的四种感染率，我们可以发现当群体佩戴口罩率下降时，由于病毒效益的挥发带来的了人群感染率的上升。其中佩戴口罩的人越少，感染率越大，在图上显示为线性图示的斜率越大。同时通过图示也可以发现当感染率超过某一阈值后，群体中的感染人数会出现饱和情况，可见当口罩率下降时由疫情带来的高峰在时间节点上会出现前移动的现象，这将给疫情防控带来极大的阻碍。因此基于以上的分析可以说明口罩作为一项重要的防疫渠道，在密接人数不变的情况下能有效缓解疫情高峰期的到来，以便政府能够拥有足够的时间应对疫情的爆发。

问题4 基于真实数据的传染病模型拟合建立

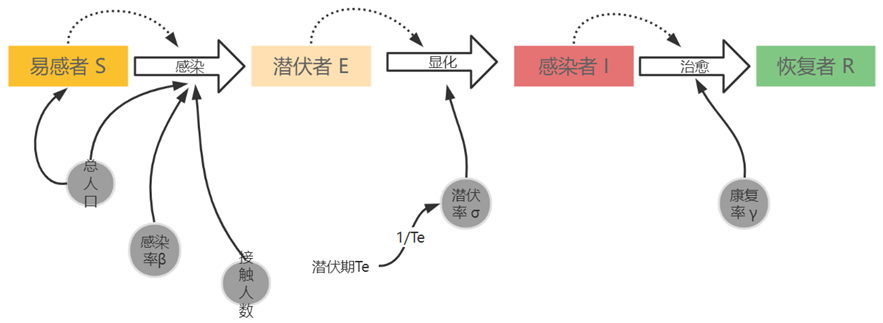
模型假设说明：
（1）在潜伏期内不具备传染性；
（2）在潜伏期中的肯定会发病，即肯定会从潜伏者转变为感染者；
（3）病毒传播处于在没有死亡或出生的封闭人群中。

模型的建立与求解：


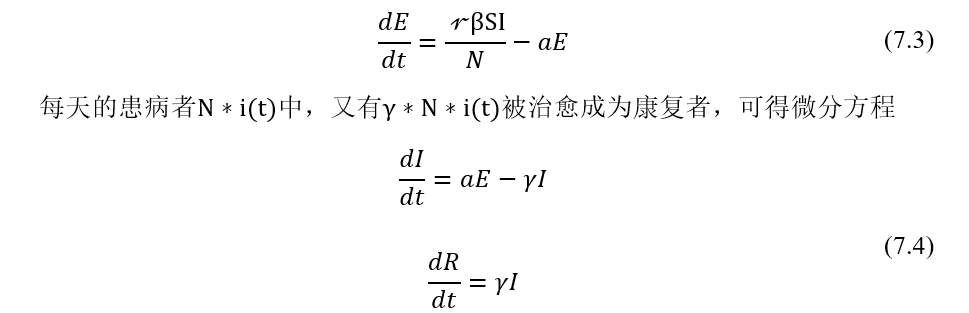
此模型无解析解，给定指定参数即可求得数值解。对此我们借助Python工具实现模型的代码逻辑。

SEIR传染病模型演变图：

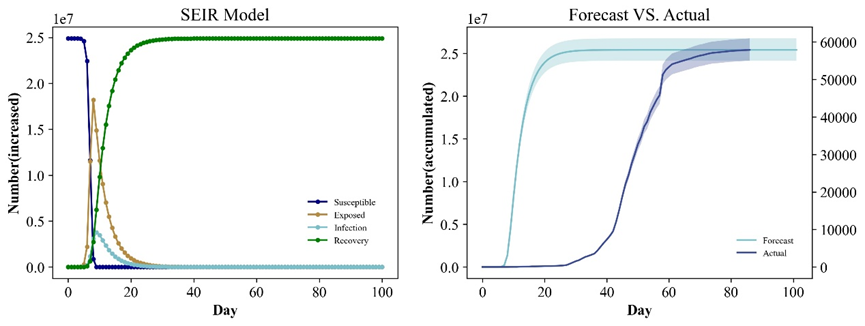
上海本轮疫情分析

3月1日至2022年5月26日的病毒流行曲线：

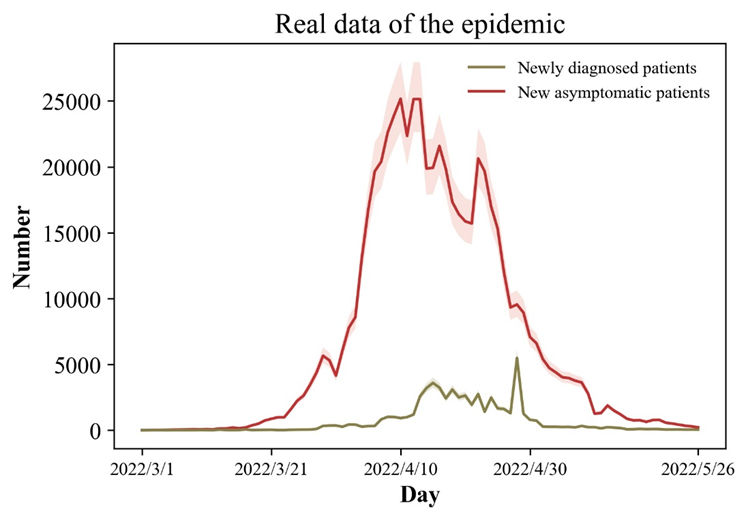
由上图可知上海本轮疫情高峰出现在4月份，其中4月8日左右新增加的无症状病例数量最多，从4月10日到4月30日，有一波新增加的确诊病例高潮。造成这个种情况的原因，主要是上海在3月底采取了积极的封城措施，使得接触人数和感染率有很大的下降，在经历一段病毒的潜伏期之后，无症状和确诊病例的人数开始下降。

提前3月20日封城疫情进展图：

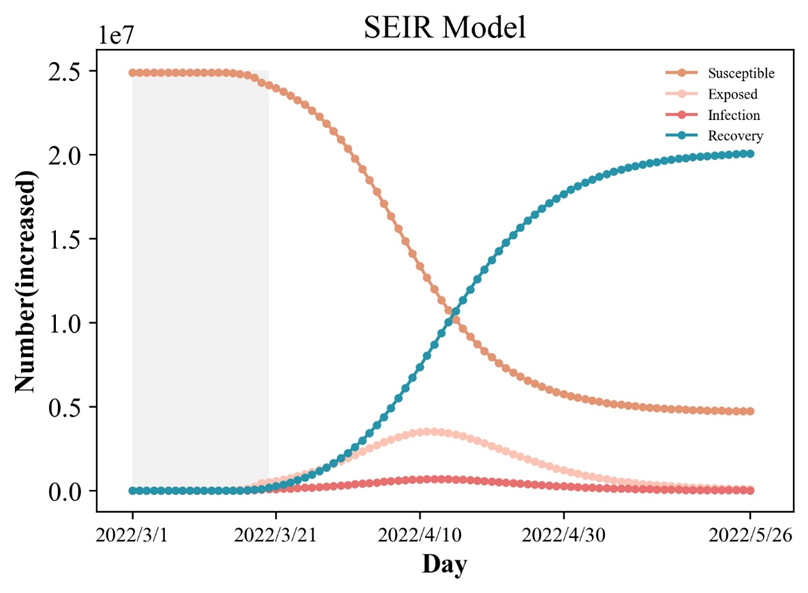
有上图可知，当封城时间提前到3月20日时，在4月15日左右疫情发生较大爆发，暴露人群和感染人群数目迅速增加，但基于中国较好的疾病救治环境康复群体数目在这段时间缓慢上升，此后感染群体经过一定的潜伏期后数量也开始下降，到4月30日左右，疫情已经基本被控制。

推迟4月10日封城疫情进展图：

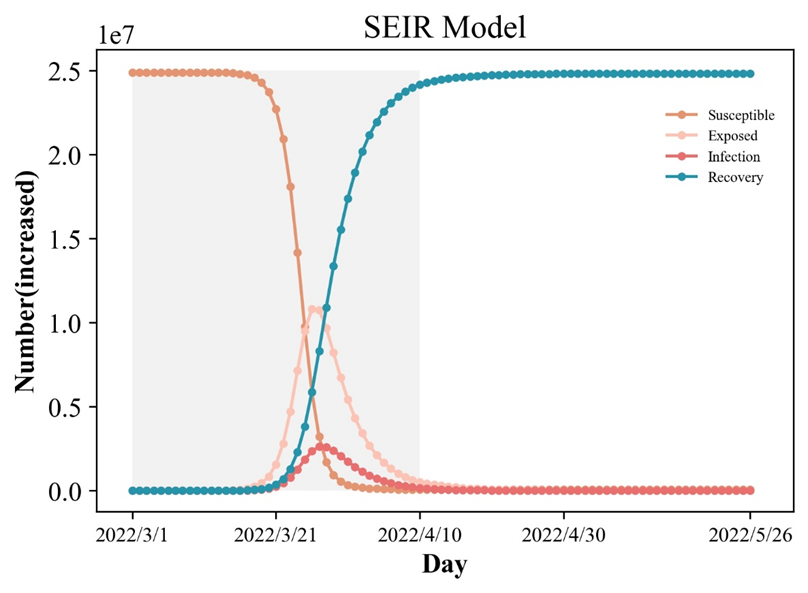
有上图可知，当封城时间推迟到4月10日时，在3月30日左右疫情发生较大转变出现爆发，暴露人群和感染人群迎来较大幅度的峰值，不过易感染人群数目减少，康复群体数目增加。直到4月10日，易感者、潜伏者和感染者数量才开始逐渐减少，完全控制疫情需要花费更多的时间。