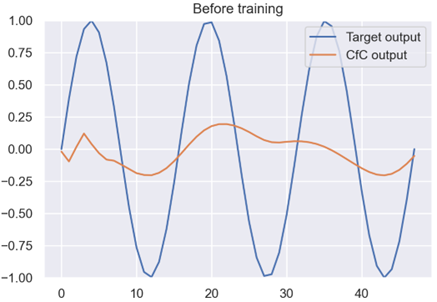
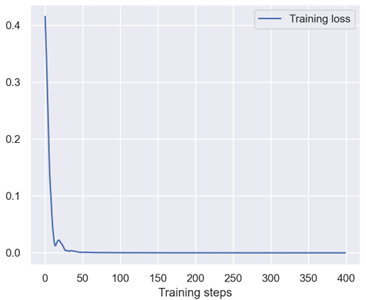
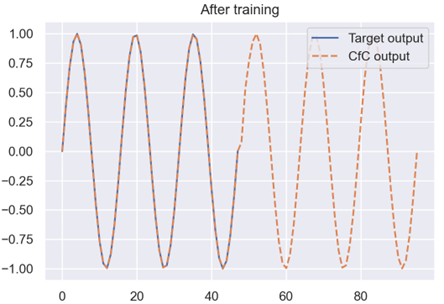
麻省理工学院(MIT)的研究者开发出了一种新型的神经网络,其不仅能在训练阶段学习,而且还能持续不断地适应。他们将这种灵活的算法命名为「Liquid」网络,因为其能像「液体」一样改变其底层的数学方程以持续适应新的输入数据。这一进展能助力基于动态变化数据的决策任务,比如医疗诊断和自动驾驶中涉及到的任务、大脑和心脏监测、天气预报和股票定价。
但是随着神经元和突触数量的增加,这些模型的计算成本变得越来越高,需要笨拙的计算机程序来解决其潜在的复杂数学问题。
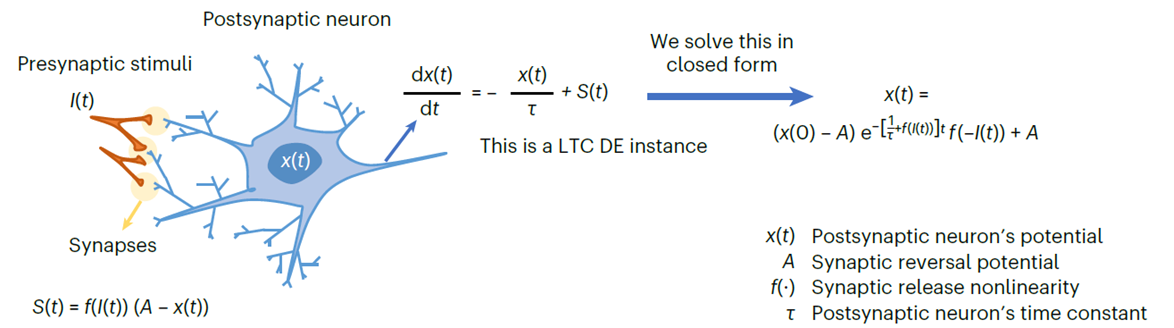
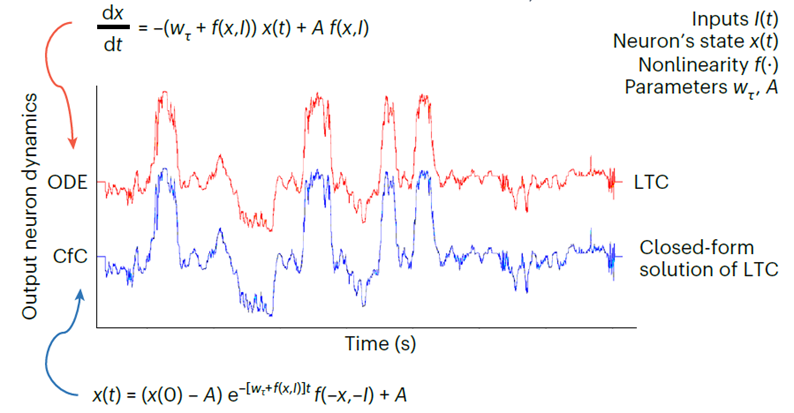
现在,同一个研究团队发现了一种缓解这一瓶颈的方法,即通过求解两个神经元通过突触相互作用背后的微分方程,解锁了一种新型快速高效的 AI 算法——「封闭式连续时间」(CfC) 神经网络。这些模型具有与液态神经网络相同的特征:灵活、因果关系、稳健性和可解释性,但速度快几个数量级且可扩展。因此,这种类型的神经网络可用于任何涉及随着时间的推移深入了解数据的任务。
由常微分方程 (ODE) 构建的连续神经网络架构,可用于对具有复杂动态的数据进行建模。这些模型将静态神经网络的深度维度和递归神经网络 (RNN) 的时间维度转换为连续向量场,从而实现非均匀采样数据的参数共享、自适应计算和函数逼近。
虽然基于 ODE 的神经网络具有精心的记忆和梯度传播设计,但由于使用了先进的数值微分方程 (DE) 求解器,它们的训练和推理速度很慢。随着数据、任务和状态空间的复杂性增加(即需要更高的精度),这就变得更加麻烦。
封闭的连续深度模型,它具有基于 ODE 的模型的建模能力,但不需要任何求解器来建模数据,CfC 在其公式中具有明确的时间依赖性,不需要数值 ODE 求解器来获得它们的时间展开。因此,它们最大限度地平衡了求解器的准确性和效率。
python3 train_physio.py
在 Physionet 数据集上训练完整的 CfC 模型train_walker.py --minimal
在 walker2d 数据集上运行直接 CfC 解决方案

下面就是跑出来的训练图,可以发现模型的效果是可以的: