人工智能课程的期末小项目,此处再复盘一下同时尝试在服务器上进行部署

一、实验目的
使用PCA进行人脸的特征识别
二、PCA基础知识及算法总结
主成分分析(Principal components analysis,PCA)是一种通过降维技术把多个变量化为少数几个主成分的统计方法,通过消除数据的相关性,找到一个空间,使得各个类别的数据在该空间上能够很好地分离,是最重要的特征提取方法之一。
❗❗❗这个小项目主要是通过PCA提取特征后计算相似度最后达到人脸识别的目的
1、基础知识
a) 内积与投影
两个维数相同的向量的内积被定义为:
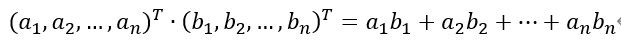
b) 基变换的矩阵表示
一般的,如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。数学表示为:
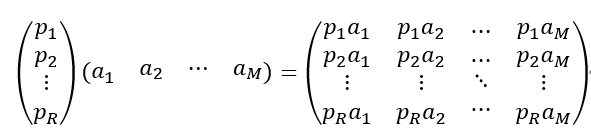
c) 方差、协方差、协方差矩阵
• 方差 - 一个字段的方差可以看做是每个元素与字段均值的差的平方和的均值,即:
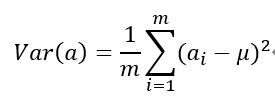
• 协方差 - 假设当μ=0时,数学上可以用两个字段的协方差表示其相关性:
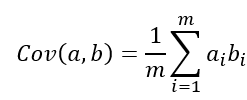
可以看到,在字段均值为0的情况下,两个字段的协方差简洁的表示为其内积除以元素数m。当协方差为0时,表示两个字段完全独立。为了让协方差为0,我们选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。
至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
• 协方差矩阵 - 设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设
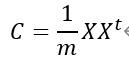
则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
d) 协方差矩阵对角化
要达到优化目前,等价于将协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列,这样我们就达到了优化目的。
2、PCA算法总结
设有m条n维数据(训练集)
- 将原始数据按列组成n行m列矩阵X
- 将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 求出协方差矩阵C=(1/m)XX^T(实对称矩阵)
- 求出协方差矩阵的特征值及对应的特征向量
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
- Y=PX 即为降维到k维后的数据
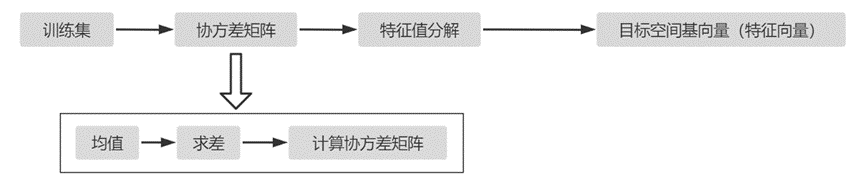
a) 训练阶段

b) 测试阶段

下图为识别结果:


三、前端网页部署
制作完前端后确保网页已经可以在本地pycharm中运行
将代码打包上传至服务器,然后解压
会遇到import自己的模块报错问题,解决方法可以看这个网站里的https://www.jb51.net/article/237114.htm,pycharm和cmd调试的方法是不一样的
能在服务器上运行flask run:
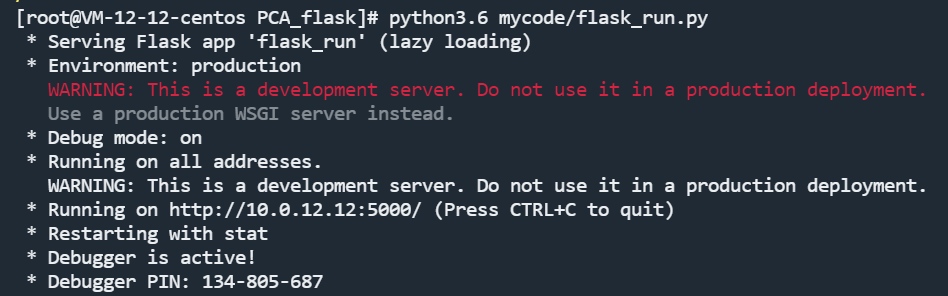
此时提到了一个警告:❗这是一个开发服务器。不要在生产部署中使用它
四、遇到的问题
1、输出平均图像
在已经成功计算出均值图像的n*1大小的mean_arr后,想要将数组转换为图像,但是却报出以下错误:

原以为是图像进行imwrite后因为灰度值的转化导致代码出错,结果进行各种尝试后都无果,仔细查看代码后发现代码中将n1大小的数组转化为了256256的数组,而观察256*256的数组后发现后面一部分的数组都为空值,最后才发现此处的height=256, width=256其实是按照输入图像的大小来规定的:

而FaceDB_orl数据集中的图像输入大小为height=112,width=92,所以此处代码要同理进行改变,最终可以成功使用cv2.imwrite保存平均图像
2、通过一个阈值来控制PCA维度
在实际应用中一般会根据投影误差选择能使误差小于0.01(99%的信息都被保留)或0.05(95%的信息都被保留)的k值,在实际编码中,参考文章《详解主成分分析PCA》,在PCA的实现过程中,对协方差矩阵做奇异值分解时,能得到S矩阵(特征值矩阵)。PCA误差的表达式等效于下式:
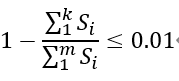
通过这个式子可以计算出PCA保留的信息量

对协方差矩阵做奇异值分解,然后不断循环尝试保留的信息是否达到了阙值:


3、读取图片为None
之前可以用cv读取图片的,但是在之后再打开发现代码会报错

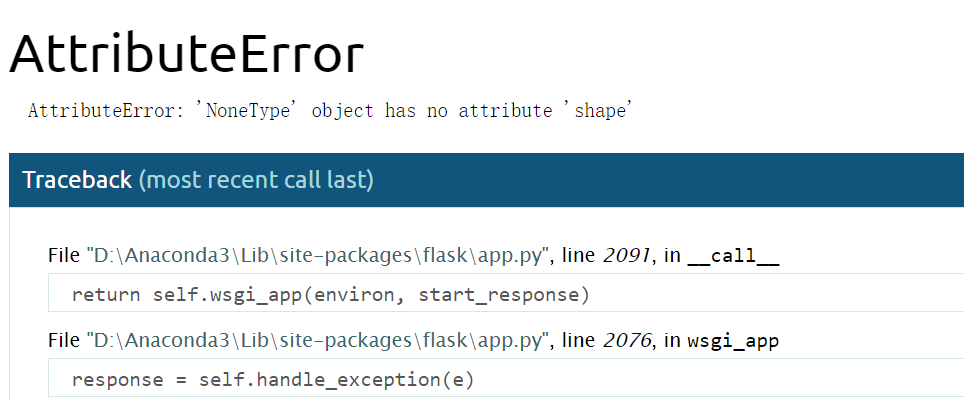
显示的是读取后的图片为None,输出后发现读取的img结果是空值,原来是修改了文件夹名称,导致文件夹中存在中文的路径,所以cv就无法正确读取图像了
❗❗❗ 使用cv2.imread(file_dir, cv2.IMREAD_GRAYSCALE)时file_dir不能出现中文
五、总结及感悟
实验代码:https://github.com/YaChen8/PCA_flask
通过PCA人脸识别的实验巩固了一些之前的线代知识点,对于PCA检测算法的整个流程更加的清晰了,特别是在第五步中求解协方差矩阵为了防止计算量过大内存溢出而采用了一种简易但又有效的方法,最后将整个PCA识别检测的功能通过Flask框架部署到Web网页端。
主成分分析是一种降维技巧,它使得我们可以使用较少的变量来描述数据,这些变量即为主成分。每个主成分都是原始变量的某种加权组合,最好的主成分可以用来改进数据分析和可视化。当信息最丰富的几个维度拥有最大的数据散度,并且彼此正交时,主成分分析能有最佳效果。
经过比较实验使用K=5进行PCA降维,基本可以比较准确的识别出人脸,对于某些无法正确识别出的,最终得到相似度最高的头像也基本和测试头像较为相似,但是实验过程还是较为粗糙,比如人脸训练集质量较好没有光照的影响,比如训练集的数量并没有很多等等。